Brown's Open Access Toolset BOAT

“The man who moves a mountain begins by carrying away small stones.” Confucius, Confucius: The Analects

CATNIP Home

Tutorial 1 - Getting Started

This tutorial details the steps needed to calculate the transfer integral from a Gaussian calculation. This tutorial assumes you have successfully installed ‘calc_J’ and you have already downloaded GAUSSIANFILES.zip and unzipped it.

To run a calculation, the executable named ‘calc_J’ must be invoked. At a minimum, you need to specify where the fort.7 files from three separate calculations have been run:

Molecule	File
MonomerA	Fort.7
MonomerB	Fort.7
Dimer_AB	Fort.7

I have relabeled these files in the example as follows

Molecule	File
MonomerA	ref.pun
MonomerB	0_2.pun
Dimer_AB	0_pair.pun

On top of the pun files you also need the log files which have been labeled as follows:

Molecule	File
MonomerA	ref.log
MonomerB	0_2.log
Dimer_AB	0_pair.log

To Calculate the transfer integral from the QC_Tools, if the .log and .pun files are located in the same folder you only have to give the path of the .pun files and the .log files will automatically be found:

calc_J -p_1 GAUSSIANFILES/0/ref.pun -p_2 GAUSSIANFILES/0/0_2.pun -p_P GAUSSIANFILES/0/0_pair.pun 

A value should be output of:

J_eff 0.0563167 eV

This is the charge transfer integral for the HOMO between the monomers. By default the HOMO will be output.

If the log file for your dimer is in a separate folder from the .pun file you can specify this explicity:

calc_J -p_1 GAUSSIANFILES/0/ref.pun -p_2 GAUSSIANFILES/0/0_2.pun -p_P GAUSSIANFILES/0/0_pair.pun -l_P GAUSSIANFILES/0/0_pair.log

To run with an arbitrary set of files simply change the respective paths.

calc_J -p_1 PATH_MonA/MonA.pun -p_2 PATH_MonB/MonB.pun -p_P PATH_DimAB/DimerAB.pun -l_P PATH_DimABLog/DimerAB.log

For a list of the correct values for the HOMO values of ethylene you can look in /GAUSSIANFILES/QC_TOOLS.dat. This file contains the transfer integral values of the HOMO of two ethylene molecules at different angles. These can be compared with the results produced by E. Valeeve et al in the /GAUSSIANFILES/angle_DeltaHOMO_2J_OrthogDeltaE.dat file.

Notice, when the angle is 0 and the molecules are symmetrically oriented with respect to each other the transfer integral can also be accurately calculated by looking in the pair.log files (Dimer of two ethylene molecules). If one takes the energies of the HOMO and HOMO-1 and divides by 2 it will yield the same value for the transfer integral as the code. This method is more commonly known as the ‘dimer splitting method’ and is based on Koopman’s theorem. This method does not however work if the molecules are not identical and symmetrically oriented with respect to each other.

Calculating the LUMO and other molecular orbital types

Additional functionality has been added to access the transfer integrals of the LUMO and other orbitals. To calculate the transfer integral of the LUMO one would use a command similar to the following.

calc_J -p_1 GAUSSIANFILES/0/ref.pun -orb_ty_1 LUMO -p_2 GAUSSIANFILES/0/0_2.pun -orb_ty_2 LUMO -p_P GAUSSIANFILES/0/0_pair.pun 

This yields:

J_eff 0.142718 eV

Note, both the monomer 1 and monomer 2 orbital types must be specified, otherwise the unspecified one will by default be the HOMO.

To calculate the transfer integral between HOMO monomer 1 and LUMO monomer 2:

calc_J -p_1 GAUSSIANFILES/10/ref.pun -orb_ty_1 HOMO -p_2 GAUSSIANFILES/10/10_2.pun -orb_ty_2 LUMO -p_P GAUSSIANFILES/10/10_pair.pun 

Giving:

J_eff -9.81153e-12 eV

Finally, if one would like to access different orbitals such as the transfer integral between the HOMO-1 of monomer 1 and LUMO+2 of monomer 2 it can be done by specifying:

calc_J -p_1 GAUSSIANFILES/40/ref.pun -orb_ty_1 HOMO -orb_num_1 -1 -p_2 GAUSSIANFILES/40/40_2.pun -orb_ty_2 LUMO -orb_num_2 2 -p_P GAUSSIANFILES/40/40_pair.pun

J_eff -0.00190564 eV

Final note on Spin

If you are dealing with restricted orbitals, then you will not need to worry about spin as only Alpha spin values will be output (which in restricted shells represents the orbitals of both spin up and down charges), by default calc_J will use the Alpha values.

However, if you are running unrestricted calculations you must make sure you know which spin values to use, either Alpha or Beta. The Gaussian program places Alpha spins higher in energy then Beta spins. So to calculate the HOMO value you would want to use Alpha spins for both monomer 1 and monomer 2 HOMO levels. For the LUMO the scenario is reversed, you would want to use the Beta spin for both monomers.

WARNING

You must pay attention to the positions of the atoms in the dimer. The atom positions cannot change for the dimer and monomer calculations. This is because the program is not smart enough to associate which orbitals belong to which atoms.

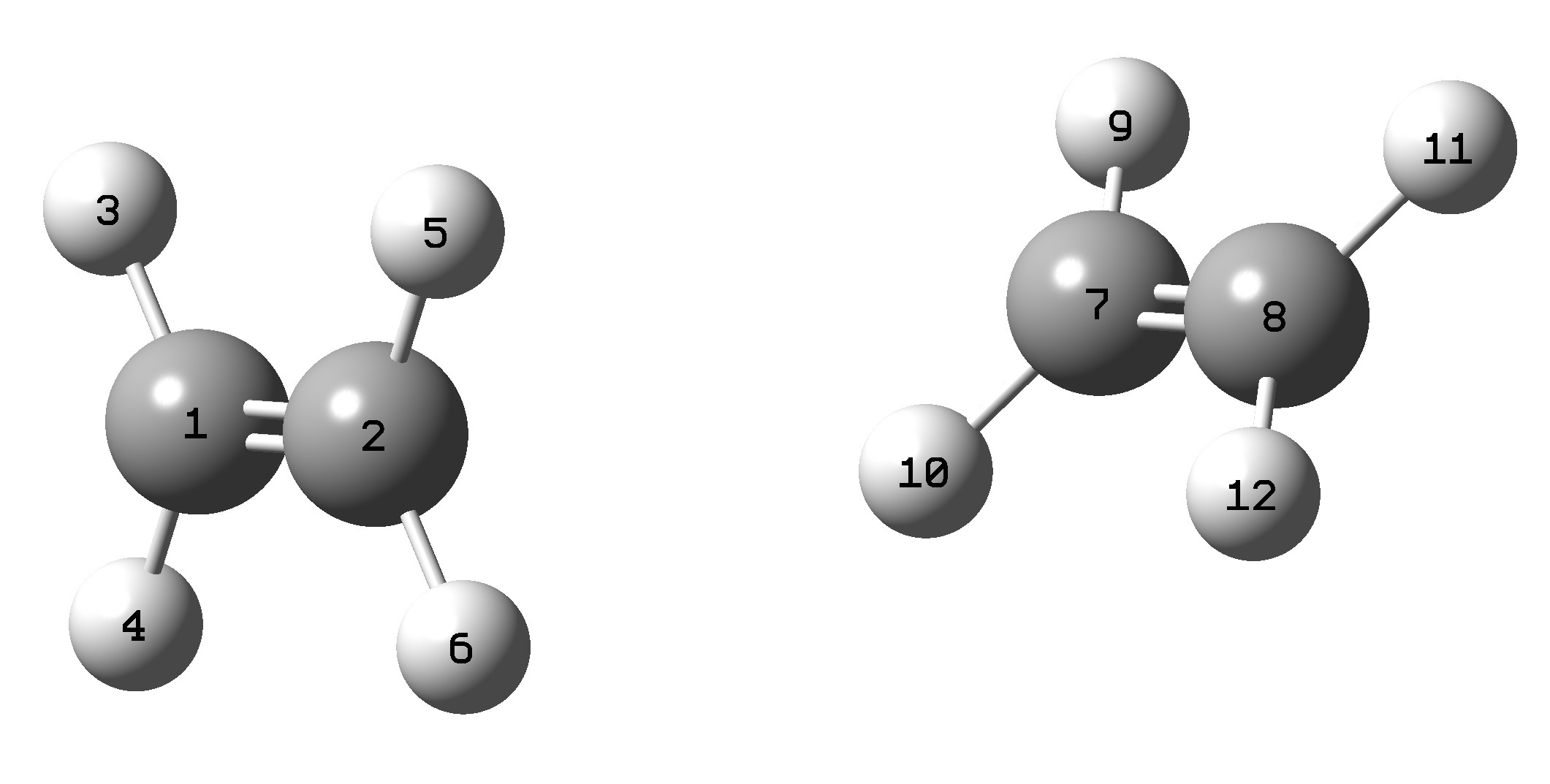
In the image shown all the atoms in the first molecule are 1-6 and the atoms in the second molecule 7-12. They must be separated in this way. The atoms must appear in the .gjf/.com file for the dimer system in this way. Such that all the atoms in the first monomer appear followed by all the atoms in the second monomer.

When you run the transfer calculation you must also pay attention to these details.

 calc_J -p_1 GAUSSIANFILES/0/ref.pun -p_2 GAUSSIANFILES/0/0_2.pun -p_P GAUSSIANFILES/0/0_pair.pun -l_P GAUSSIANFILES/0/0_pair.log

-p_1 must be associated with the first set of atoms
-p_2 must be associated with the second set of atoms

Note

The above warning is no longer necessary if the pop=full keyword is used in the Gaussian input files. This outputs the arrangement of the basis functions in the .log files. calc_J is then able to automatically line up the appropriate basis functions with the appropriate atoms.

However, because this requires the program to sort through the atoms and coefficients it might take noticeably longer for large molecules.

Extra information

If you are interested in how the different output files are used to actually calculate the charge transfer integral, you can look in the GAUSSIANFILES/10 folder. I have created a matlab file that explicitly shows where the coefficients go. If you run it you should observe the same result as is generated by the compiled cpp code.